Construcción de un Rombo y Romboide: Exploración y Ejemplos Reveladores

En el mundo de la geometría, las formas fascinantes del rombo y el romboide cautivan las mentes desde hace siglos. Estas figuras notables presentan características únicas y aplicaciones intrigantes, lo que las convierte en elementos esenciales en el reino de las matemáticas. Este artículo se adentra en el intrigante proceso de construir estas formas, guiándonos a través de métodos probados y ejemplos reveladores. Al explorar sus propiedades geométricas, comprenderemos la esencia de estas figuras y su importancia duradera.

¿Cómo se calcula el área de un rombo y un romboide?

Cómo calcular el área de un rombo

El rombo es un paralelogramo con cuatro lados iguales y dos diagonales que se cortan perpendicularmente. Para calcular el área de un rombo, se multiplica la mitad de una diagonal por la mitad de la otra diagonal.

Fórmula:

Área = (d1/2) * (d2/2)

Donde:

* d1 es la longitud de una diagonal
* d2 es la longitud de la otra diagonal

Cómo calcular el área de un romboide

El romboide es un paralelogramo con lados opuestos paralelos, pero no iguales. Para calcular el área de un romboide, se multiplica la base por la altura.

Fórmula:

Área = base * altura

Donde:

* base es la longitud del lado paralelo a la altura
* altura es la distancia perpendicular entre los lados paralelos

¿Cómo demostrar que es un romboide?

Para demostrar que una figura es un romboide, se deben comprobar las siguientes propiedades:

* Lados opuestos iguales: Los lados opuestos de un romboide deben tener la misma longitud.
* Ángulos opuestos suplementarios: Los ángulos opuestos de un romboide deben sumar 180 grados.
* Diagonales bisectrices de ángulos opuestos: Las diagonales de un romboide deben bisecar (dividir en dos partes iguales) los ángulos opuestos.

Pasos para demostrar que una figura es un romboide:

1. Medir los lados: Mide los cuatro lados de la figura. Si los lados opuestos tienen la misma longitud, pasa al paso 2.

2. Medir los ángulos: Mide los cuatro ángulos de la figura. Si los ángulos opuestos suman 180 grados, pasa al paso 3.

3. Comprobar las diagonales: Dibuja las dos diagonales de la figura. Si las diagonales bisecan los ángulos opuestos, entonces la figura es un romboide.

Ejemplo:

Consideremos una figura con los siguientes datos:

* Lados: AB = 6 cm, BC = 6 cm, CD = 4 cm, AD = 4 cm
* Ángulos: ∠A = 100°, ∠B = 80°, ∠C = 100°, ∠D = 80°
* Diagonales: AC y BD

Demostración:

* Lados opuestos iguales: AB = CD = 6 cm, BC = AD = 4 cm.
* Ángulos opuestos suplementarios: ∠A + ∠C = 100° + 100° = 200° (mayor que 180°)
* Diagonales bisectrices de ángulos opuestos: No se cumple, ya que las diagonales no bisecan los ángulos opuestos.

Conclusión:

Como no se cumple la propiedad de los ángulos opuestos suplementarios, la figura no es un romboide.

¿Cómo descubrir un rombo?

Cómo descubrir un rombo

1. Definición de rombo:
Un rombo es un paralelogramo que tiene los cuatro lados iguales. Es decir, es una figura geométrica de cuatro lados iguales que tiene forma de diamante.

2. Propiedades de un rombo:

• Los lados opuestos son paralelos y congruentes.
  

• Las diagonales son perpendiculares y se bisecan mutuamente.
  

• Las diagonales dividen el rombo en cuatro triángulos rectángulos congruentes.

3. Métodos para descubrir un rombo:

a. Medición de lados y diagonales:

• Mide los cuatro lados del paralelogramo. Si todos los lados son iguales, es un rombo.
  

• Mide las dos diagonales del paralelogramo. Si las diagonales son perpendiculares y se bisecan, es un rombo.

b. Propiedades de un paralelogramo:

• Si un paralelogramo tiene diagonales perpendiculares, entonces es un rombo.
  

• Si un paralelogramo tiene diagonales que se bisecan mutuamente, entonces es un rombo.

c. Propiedades geométricas:

• Si un paralelogramo tiene un ángulo de 90 grados, entonces es un rombo.
  

• Si un paralelogramo tiene ángulos congruentes, entonces es un rombo.

d. Coordenadas de los vértices:

• Si las coordenadas de los vértices opuestos de un paralelogramo son simétricas respecto del origen, entonces es un rombo.

4. Ejemplos:

- Un cuadrado es un rombo especial que tiene todos los lados y ángulos iguales.

• Un rectángulo que tiene diagonales perpendiculares es un rombo.
  

• Un paralelogramo que tiene ángulos iguales de 60 grados es un rombo.

¿Cuál es la diferencia entre un rombo y un romboide?

Rombo

* Cuadrilátero con los cuatro lados iguales.
* Tiene dos pares de lados paralelos.
* Sus diagonales son perpendiculares y se cortan en el centro.
* Sus ángulos opuestos son iguales.
* Es un paralelogramo.

Romboide

* Cuadrilátero con dos pares de lados paralelos.
* Sus diagonales se cortan en el centro.
* Sus ángulos opuestos no son necesariamente iguales.
* No es necesariamente un paralelogramo.

Diferencias entre un rombo y un romboide

* Igualdad de lados: El rombo tiene los cuatro lados iguales, mientras que el romboide no necesariamente.
* Ángulos opuestos: En un rombo, los ángulos opuestos son iguales, mientras que en un romboide no necesariamente.
* Paralelogramo: El rombo es siempre un paralelogramo, mientras que el romboide no necesariamente.

Preguntas Frecuentes

¿Cuál es la diferencia entre un rombo y un romboide?

Un rombo es un paralelogramo con los cuatro lados iguales, mientras que un romboide es un paralelogramo con lados opuestos iguales.

¿Cuáles son las propiedades geométricas de un rombo?

Un rombo tiene las siguientes propiedades:

• Cuatro lados iguales
  

• Diagonales perpendiculares que se bisecan
  

• Ángulos opuestos iguales
  

• Esquinas equidistantes del centro

¿Qué fórmulas se pueden utilizar para calcular las áreas y perímetros de un rombo?

El área de un rombo se puede calcular como:
Área = Diagonal 1 × Diagonal 2 / 2

El perímetro de un rombo se puede calcular como:
Perímetro = 4 × Longitud del lado

¿Cuáles son algunos ejemplos de aplicaciones prácticas de rombos y romboides en la vida real?

Los rombos y romboides se utilizan en varias aplicaciones, que incluyen:

• Formas arquitectónicas (tejas, ventanas)
  

• Patrones de acolchado y tejido
  

• Diseño de logotipos y marcas
  

• Mosaicos y patrones decorativos

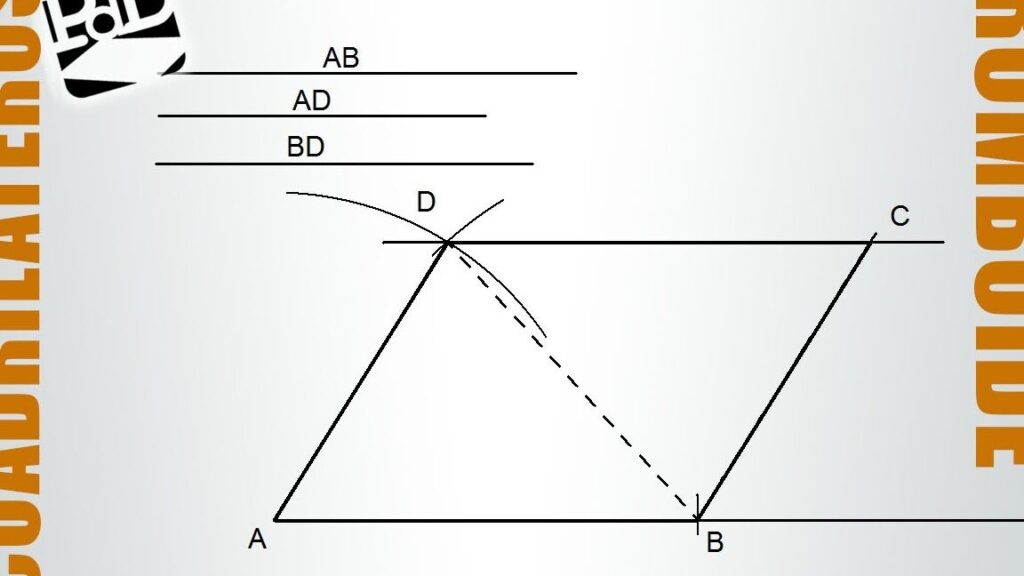
¿Cómo se dibuja un rombo o un romboide?

Para dibujar un rombo:

• Dibuja un cuadrado y luego alarga o acorta dos lados opuestos para crear ángulos agudos y obtusos.

Para dibujar un romboide:

• Dibuja un paralelogramo y luego alarga o acorta un par de lados opuestos para crear una forma no cuadrada.

Si quieres conocer otros artículos parecidos a Construcción de un Rombo y Romboide: Exploración y Ejemplos Reveladores puedes visitar la categoría Matemáticas y Física.